4.2 Uso de la escala gráfica
En primer lugar veamos qué es:
La escala es la relación matemática que existe entre las dimensiones reales y las del dibujo que representa la realidad sobre un plano o un mapa.
En los planos y mapas reales siempre aparece una escala que relaciona las medidas que se muestran en ellos con las medidas reales.
Existen tres formas de representar la escala:
- Escala gráfica: es la representación dibujada de la escala unidad por unidad, donde cada segmento muestra la relación entre la longitud de la representación y el de la realidad. Un ejemplo de ello sería: 0_________10 km
- Escala numérica como un cociente de la unidad entre otro número. Un ejemplo sería 1:25 ó 1:50.000, lo cual significa que 1 unidad del mapa equivale a 25 ó a 50.000 unidades en la realidad.
- Escala unidad por unidad: es la igualdad entre dos longitudes: la del mapa (a la izquierda del signo "=") y la de la realidad (a la derecha del signo "="). Un ejemplo de ello sería 1 cm = 4 km; 2cm = 500 m, etc.
Las escalas pueden ser:
-
- Escalas de ampliación: 100:1, 50:1, 20:1, 10:1, 5:1, 2:1
- Escala natural: 1:1
- Escalas de reducción: 1:2, 1:5, 1:10, 1:20, 1:50, 1:100, 1:200, 1:500, 1:1000, 1:2000, 1:5000, 1:20000
Nosotros vamos a practicar con las de reducción, es decir cosas muy grandes las vamos a representar más pequeñas.
Vamos a trabajar con las escalas:
Una escala de 1:50:
- Quiere decir que podemos representar 50 m en la realidad dibujando 1 m en el plano,
- ó 5 m como 0,1 m, (1 dm),
- ó 0,5 m como 0,001 m = 1 cm en el plano.
Observarás que la relación en todos los casos es que el dibujo es 50 veces menor que la medida real.
- Si quisiésemos representar por ejemplo, 4,50 m (reales) a escala 1:50, en el plano, lo haríamos con la siguiente representación:
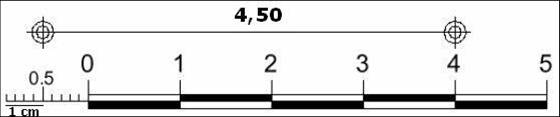
- Si quisiésemos calcular el valor numérico de 4,5 m en el plano lo obtenemos mediante una regla de tres:
1 unidad en el plano ---------------- a 50 unidades en la realidad
x unidad en el plano ---------------- a Y unidades en la realidad
Los valores de la izquierda representan valores del plano y están uno debajo del otro. Los de la derecha representan valores de la realidad. Conviene tener siempre presente dónde colocamos cada uno para no confundirnos.
La regla dice que "multipliquemos en cruz " y nos quedará: 50 . x = 1 . y
En nuestro ejemplo la regla de 3 quedaría así: y = 4,5 m
1 m ---------------- 50 m
x m ---------------- 4,5 m
50 . x = 1 . 4,5 si despejamos, x = 4,5/50 = 0,09 m = 9 cm
4,5 m en la vida real a escala 1:50 representan 9 cm en el plano
Por tanto, como puedes deducir, la escala es un factor de conversión entre el plano y la realidad:
- Si queremos pasar del plano a la realidad tenemos que aumentar el tamaño, por lo que multiplicaremos las medidas por la escala.
- Al revés, si queremos pasar de lo real al plano tendremos que reducir, dividir las medidas por la escala.
Según qué vayamos a representar y cuánto detalle necesitemos, será más adecuada una escala que otra:
- A escala de 1:1.000 y 1:5.000 se pueden estudiar muchos detalles.
- Entre 1:5.000 y 1:20.000, planos y callejeros de ciudades.
- Entre 1:20.000 y 1:50.000, comarcas y municipios.
- Entre 1:50.000 y 1:200.000 provincias y regiones.
- Entre 1:200.000 y 1:1.000.000, regiones y países.
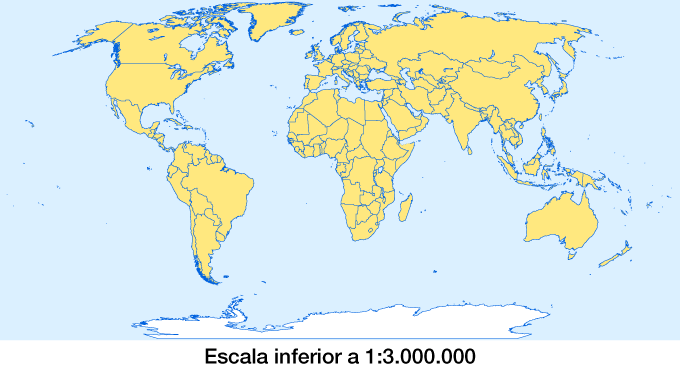
- A escalas inferiores a 1:1.000.000 continentes y hasta el mundo entero.
Hay planos en los que no se refleja la escala numérica, pero sí la barra. En ellos tendremos que medir la barra y averiguar a cuánto equivale en la realidad. Por ejemplo, en el siguiente mapa de Galicia:
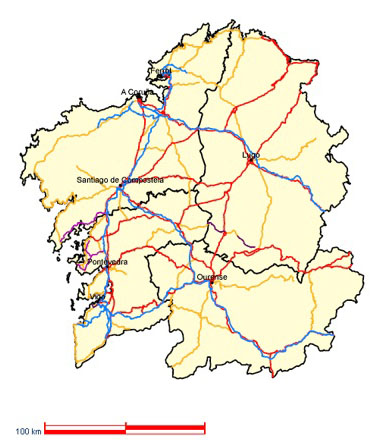
En este caso, 100 km en la realidad equivalen a 4 cm en el plano (lo hemos medido con la regla y nos ha dado que la barra mide 4 cm)
4 cm plano ---------------- 100 km = 100 x 100000 = 10000000 cm en la realidad
1 cm plano ---------------- x cm en la realidad
x= 10.000.000/4 = 2.500.000 La escala sería 1:2.500.000
Para calcular superficies la situación es parecida y podemos hallar la superficie en el plano y pasarla a la realidad con la escala o hallar las dimensiones en la realidad y hallar entonces la superficie. Da igual.
Los planos 3D obtenidos en el ordenador vistos antes son muy parecidos a las Maquetas, pero éstas son reproducciones reales en 3D a escala de objetos, edificios, incluso ciudades como la de Madurodam.
Sus escalas son especiales:
- Para figuras o vehículos militares 1:16; 1:35 ó 1:48.
- Para el aeromodelismo 1:32 ó 1:72.
- Para el modelismo naval desde 1/700 hasta 1/72.
- Para maquetas de viviendas la escala va desde 1:20, (con mucho detalle),
- Hasta 1:750 para grandes edificios.

Imagen: MEC-ITE
En La Haya, Holanda, existe una ciudad completa a escala 1:25. Se trata de MADURODAM, donde se han construído en maquetas los edificios más representativos de Holanda y también sus canales, como se puede ver en la fotografía siguiente:

Imagen: flickr.com. Przemek Siemion
