Para aprender hazlo tú.

Vamos a practicar un poco, es la mejor forma de aprender:
- Empecemos a practicar con cambios de unidades de longitud, unidades de tiempo y de área. ¡Verás que fácil es!
- Recordemos el SI
- Sigamos con la notación científica
- Calculemos el valor real de un objeto y los errores cometidos.
- Por último una cuestión de planos y escala
A ver cómo se nos dan estos cambios con las unidades de longitud, de área y de tiempo. Para ello debes recordar que para subir en las escaleras de las unidades hay que dividir (entre 10 , 100, o 60) y para bajar la escalera multiplicar:

mm2 equivale a 0,01 m2
dam son 800000 mm
cm2 equivale a 400 mm2
5 hm son dm
mm son 0,3 m
30000 cm2 equivale a dam2
2.678.400 s son días
m son 1 km
m2 equivale a 1 dam2
0,5 cm son mm
min son 6 h
s son 20 h
h son 1440 min
km2 equivale a 2 hm22|
La distancia a recorrer es 6550 m, tarda 2 horas en llegar, sí llega a tiempo.
| |
|
La distancia supera los 11 Km, ¡ qué pena, no llega!
|
Verdadero Falso
Vamos a repasar el sistema internacional de unidades (SI). Para lo cual vamos a rellenar los siguientes huecos, para lo cuál deberá utilizar las siguientes palabras o símbolos:
Temperatura, Longitud, Metro, Segundo, Kilogramo, s,
| Magnitud | Unidad | Símbolo |
|
|
m |
|
| Masa |
|
kg |
| Tiempo | ||
| Grado Kelvin |
K |
Completa los siguientes ejercicios con los datos que faltan en los recuadros, pero antes deberías repasar el apartado de notación científica.

2.- Un virus tiene una longitud de 80 Å (Armstrong). Al ponerlo en el S.I. : 1 Å = 0,1 nm = 0,0001 ![]() = 0,0000001 mm = 0, 0000000001 m = 1x10-10 m // 80 Å =
x10
m
= 0,0000001 mm = 0, 0000000001 m = 1x10-10 m // 80 Å =
x10
m
3.-Expresa en notación científica o decimal según los casos los siguientes datos:
4000 = 4 x 1000 = x 10
798,2 = 7,982 x 10
= 7,09 x 10-3
12345 = x 10
–0,003456 = x 10
Hemos realizado 4 medidas de la altura de una mesa con un metro (que mide milímetros, es decir, décimas de cm).
Las medidas obtenidas son: A) 60,2 cm; B) 60,3 cm; C) 59,9 cm y D) 60,9 cm.
1º. Vamos a calcular en primer lugar el valor real y elegir la opción correcta, la 1 o la 2:
| 1 |
60,32 cm
|
| 2 |
60,3 cm
|
| 1 |
A)|60,2 - 60,3|= 0,1 B)|60,3 - 60,3|= 0 C)|59,9 - 60,3|= 0,4 D)|60,9 - 60,3|= 0,6 |
| 2 |
A)|60,3 - 60,2|= 0,1 B)|60,3 - 60,3|= 0 C)|60,3 - 59,9|= 0,4 D)|60,3 - 60,9|= 0,6 |
3º. ¿Te atreves a calcular el error relativo?
¿Qué opción es la correcta, la 1 o la 2?
| 1 |
A) 0,2 % B) 0% C) 0,7% D) 1% |
| 2 |
A) 99,8% B) 100% C) 99,3% D) 99% |
Esta pregunta no es difícil, es una situación que se nos plantea cuando vamos a comprar un piso o casa y nos dan el plano, a escala, debemos con la escala averiguar si la información que nos dan en la agencia es cierta.
La escala nos dice cuantas veces esa medida es más grande en la realidad o cuántas veces es más pequeña en el plano.
Imagina que este plano pueda ser el tu próxima vivienda, y cómo es natural quieres saber si podrás colocar los muebles que ya tienes en tu otra casa.
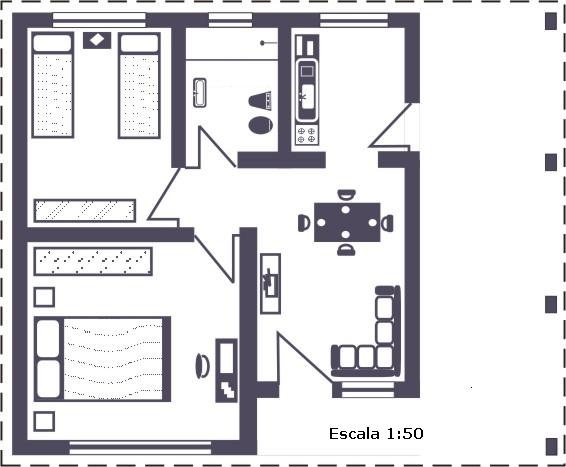
Con una regla hemos obtenido estas medidas:
- Las medidas del salón en el plano son: 10 cm de largo y 6 cm de ancho.
- Las del dormitorio principal son:8 cm de largo por 8 cm de ancho.
- Las de la cocina son 6 cm x 6 cm.
- Las del otro dormitorio son 8 cm por 6 cm.
- El baño es pequeño mide 6 cm por 4 cm.
Y ahora teniendo en cuenta la escala (1:50) averiguar las medidas reales.
Conociendo estos datos vamos a ver si somos capaces de rellenar los espacios en blanco con los datos correctos:
Creo que en el salón a lo mejor tendré problemas porque tiene
m2 , y el sofá rinconera de 4 m por 2 m puede que no quede bien, porque la pared más pequeña del salón mide
m, y está la puerta a a terraza.
Lo que tengo duda si el armario ropero del dormitorio principal cogerá en la pared del fondo, ya que mide 3,5 m, y la puerta ocupa 1 m de esa pared que mide m. Aunque el dormitorio mide m2 voy a tener problemas.
La cocina la tengo que encargar, voy a poner todos los muebles en la única pared que no tiene ni puerta ni ventana, como mide m esa parded, podré poner pocos muebles, y en la esquina pondré una mesa porque aunque sólo tiene m2 es suficiente.
Dónde no tengo dudas es en el otro dormitorio, es grande tiene
m2, y la pared del fondo que mide
m, se puede poner un armario de 2m sin que estorbe la puerta.
Aunque el baño tiene sólo m2 cabe en el fondo una bañera de m de larga, pues ocupa toda la pared.


