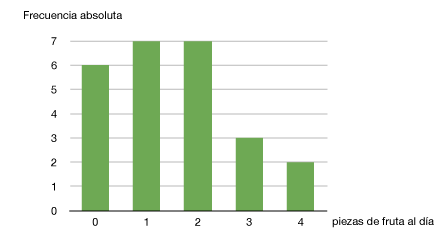
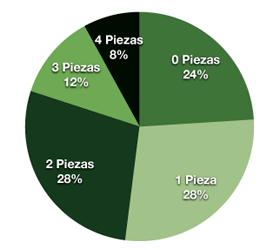
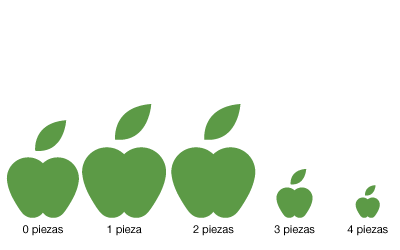
3.3.- ¿Cómo podemos ver los datos gráficamente?

Los datos estadísticos se pueden "ver" en dibujos. Sí sí, en serio. ¿A que si lo logramos será genial? Vamos allá.

Diagrama de Barras:

Un diagrama de barras de una variable estadística se hace de forma muy sencilla. Por pasos, tras hacer la tabla de frecuencias:

  • Primero dibujamos dos ejes de coordenadas.
  • Después colocamos los valores de la variable en el eje x. Deben ser valores de variable discreta.
  • Por último levantamos una barra sobre cada valor. ¿Hasta qué altura? Hasta lo que indiquen las frecuencias (absolutas o relativas).

Por ejemplo, en el caso anterior, a partir de la tabla podemos obtener el diagrama de barras siguiente:

Diagrama de barras

Icono IDevice Actividad

Así que

Un diagrama de barras se construye dibujando barras sobre los valores, que midan lo que indiquen las frecuencias absolutas (o relativas).


Diagrama de sectores

Un diagrama de sectores es un círculo dividido en sectores cuya área será tanto mayor cuanto mayor sea la frecuencia del valor que representa.

  • Dibujamos un círculo.

  • Lo dividimos en tantos sectores circulares ("quesitos") como valores queramos representar. Pero claro, al valor con mayor frecuencia le corresponderá una parte más grande ¿verdad?

  • Para cada valor su sector tendrá un ángulo PROPORCIONAL a su frecuencia. ¿Que te has asustado? Vamos a ver cómo hacerlo que es fácil, sólo hay que hacer una "regla de tres". El círculo abarca 360º ¿verdad? pues bien:

    • repartimos los 360º entre el total de respuestas que, en nuestro ejemplo, es 10. 360º : 10 = 36º grados para respuesta.

    • si cada respuesta se representa con un sector ("quesito") de 36º el valor 0 que se repitió en cuatro respuestas se representará con un sector de 4X36 = 144º. Y así con el resto de valores.

Haciendo esto, obtenemos el siguiente diagrama de sectores:

Valores Frecuencia  
0 4 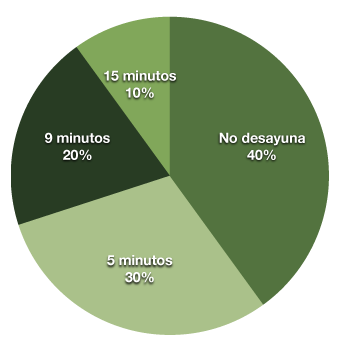Diagrama de sectores
5 3
9 2
15 1

El cálculo que hemos tenido que hacer es:

360º:10 = 36º (Para ver cuántos grados corresponden a cada respuesta individual)

36x4 = 144º; 36x3 = 108º; 36x2 = 72º; 36x1 = 36º (Para ver cuántos grados le corresponde a cada dato según su frecuencia).

Icono IDevice Actividad

Recuerda:

Para saber el ángulo que tiene que ocupar cada sector, dividimos 360º entre el número de respuestas y multiplicamos lo obtenido por la frecuencia absoluta de cada valor.


Pictograma

En este caso representamos cada valor con un dibujo alusivo cuyo TAMAÑO dependerá de la frecuencia absoluta (o relativa) del valor.

Por ejemplo, ya que estamos con el tiempo dedicado a desayunar, representaremos cada valor con una taza con reloj, que será más grande para las respuestas más frecuentes y menor para las respuestas menos frecuentes.

Pictograma

Icono IDevice Pre-conocimiento

Pero cuidado

Si con tamaño nos referimos al área, entonces a doble frecuencia no corresponde doble tamaño, si no 4 veces el tamaño, porque la relación es cuadrática (un área se calcula elevando a cuadrado una longitud) y el dibujo obtenido no se corresponderá con los datos.

Por tanto, tenemos que dejar claro a qué nos referimos con tamaño. Podemos quedar en que a doble, triple… frecuencia corresponda doble, triple… altura del dibujo, por ejemplo.


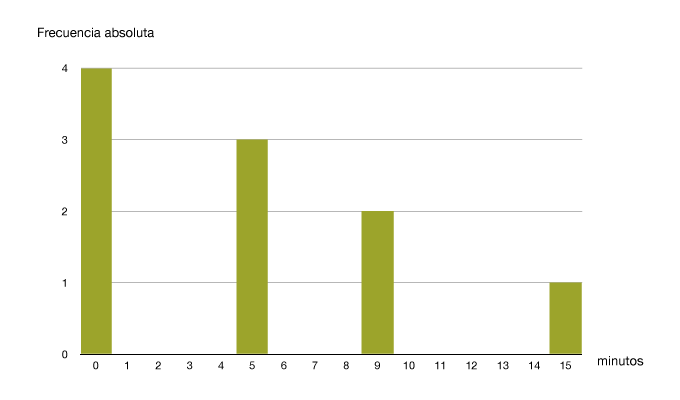
Histograma

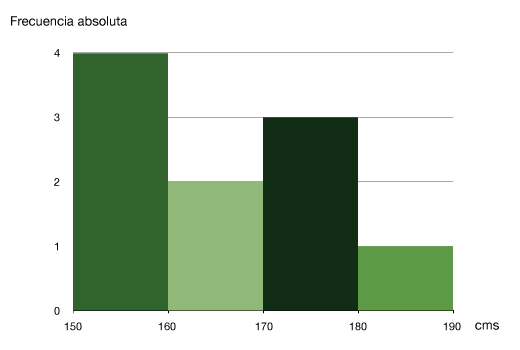
Un histograma es muy similar a un diagrama de barras, solo que se usa para variables cuyos datos se agrupan en intervalos. Por ejemplo, si preguntamos a nuestros vecinos por su estatura, la tabla de frecuencias puede ser esta:

Valores de la variable (estatura en cm) Ii Frecuencias absolutas ni Frecuencias relativas fi Frecuencias absolutas acumuladas Ni Frecuencias relativas acumuladas Fi
150-160 4 0,4 4 0,4
160-170 2 0,2 6 0,7
170-180 3 0,3 9 0,9
180-190 1 0,1 10 1
  10 1    

¿Has visto algo nuevo en esta tabla? Seguro que te has dado cuenta de que en la primera columna no aparecen datos concretos de altura, sino los intervalos en que agrupamos los valores y las frecuencias absolutas se refieren al número de personas cuya altura está dentro del intervalo correspondiente.

Pues bien, para hacer el histograma:

  • Primero dibujamos dos ejes de coordenadas.

  • Después colocamos los intervalos en el eje X.

  • Por último levantamos un rectángulo sobre cada intervalo. ¿Hasta qué altura? Pueden ocurrir dos cosas:

    • que todos los intervalos tengan la misma amplitud (como en nuestro caso, que todos "van de 10 en 10")

    • que haya intervalos más amplios que otros. Este caso lo dejaremos de momento.

  • En el primer caso, la altura del rectángulo será la indicada por la frecuencia (absoluta o relativa) correspondiente.

En nuestro último ejemplo:

Histograma para el último ejemplo

Icono IDevice Objetivos

Para saber más…

Los intervalos en los que se agrupan los valores de una variable continua o discreta con demasiados valores se llaman intervalos de clase.

El valor representante de un intervalo de clase se llama marca de clase y suele coincidir con el valor medio del intervalo (con el dato que queda justo en medio del mismo).


Icono IDevice Pre-conocimiento

Interesantes ejemplos de gráficos

En este enlace tienes una presentación con muchos gráficos estadísticos. Es una encuesta sobre salud nacional realizada en 2006 (Ministerio de Sanidad). ¡No tienes que aprenderte ninguno...! Son solo ejemplos para que veas cómo los gráficos estadísticos se usan con mucha "frecuencia".


Icono IDevice Actividad de Lectura

Autoevaluación


Realiza los gráficos estadísticos que puedas para la variable trabajada en la anterior autoevaluación. Te recordamos la tabla de frecuencias:

xi ni fi Ni Fi
0 6
 0.24
 6
 0.24
1
 7
 0.28
 13
 0.52
2
 7
 0.28
 20
 0.8
3
 3
 0.12
 23
 0.92
4
 2
 0.08
 25
 1
total 25 1