2.- Al andar se hace camino
Caminante, son tus huellas
el camino y nada más;
caminante, no hay camino,
se hace camino al andar.Al andar se hace camino
y al volver la vista atrás
se ve la senda que nunca
se ha de volver a pisar.
Antonio Machado
(Sevilla 1875 - Collioure (Francia) - 1939)
Ya lo decía el poeta.
¡Y qué razón tenía! Cuando tengas ocasión, detente a observar lo cerros del campo y verás cuántas veredas se han hecho a base de pasar una y otra vez por el mismo sitio…
De eso te vamos a hablar en este apartado… de caminos, de veredas, de… trayectorias.
Si un cuerpo que se mueve fuese dejando un rastro, iria dibujando una línea; una línea formada por todos los puntos por los que va pasando. Esa línea es la trayectoria del movimiento.
La trayectoria es la línea imaginaria que "dibuja" un cuerpo al moverse
Hay muchas trayectorias que quedan marcadas: una carretera, la vía de un tren, un río, una vereda, la estela de un avión… son "lineas" que marcan el sitio por donde se mueve o se ha movido un cuerpo.
Pero lo normal es que un cuerpo se mueva "sin dejar rastro" de por donde pasa, por eso decimos que la trayectoria es una línea imaginaria.
La importancia de las trayectorias

Imagen: © Sportgraphic | Dreamstime.com
Predecir trayectorias es algo que hacemos continuamente, sin darnos cuenta. Sin ir más lejos, por ejemplo, cuando pensamos cuál es el mejor camino para ir de un sitio a otro. Pero claro, no hacemos cálculos para eso ¿verdad? Tampoco hace cálculos el futbolista cuando "calcula" la trayectoria del balón antes de lanzar un libre directo, o el piloto de fórmula 1 cuando piensa la "trazada" de una curva.
Otras veces sí que son necesarios cálculos, y cálculos muy importantes. Piensa, por ejemplo en la importancia de calcular bien a trayectoria que debe seguir un cohete que se dirija a la estación espacial internacional. O la trayectoria que va a seguir un huracán, como las de la imagen de abajo, donde puedes ver algunas de las posibles trayectorias que se calcularon para el movimiento del huracán Ike en septiembre de 2008.
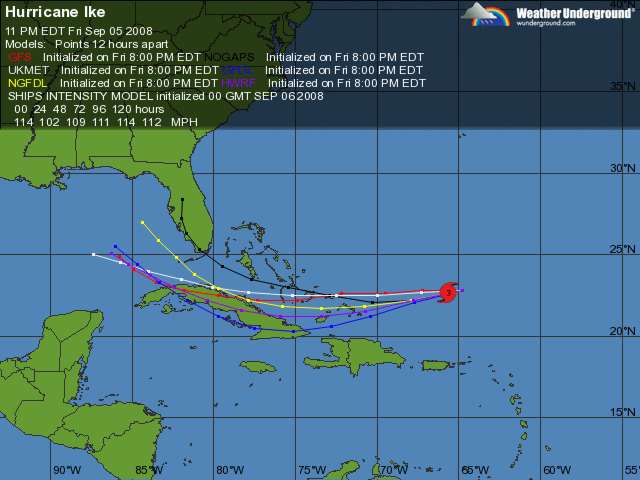
Imagen: Weather undergound
La trayectoria que sigue un cuerpo puede ser bastante complicada; piensa, por ejemplo, en la trayectoria que sigue una abeja mientras vuela. Pero también hay movimientos cuyas trayectorias son muy sencillas, fáciles de estudiar: rectas, circunferencias o parábolas son las más sencillas.
 |
 |
 |
| La luz del láser describe un movimiento rectilineo | La rueda de la noria describe un movimiento circular | Los chorros de esta fuente describen un movimiento parabólico |
Imágenes: Stock Xchng / Flickr.com (Photo Plod y joemacr)
Autoevaluación
¿Cuál crees que será la trayectoria de los movimientos que se indican en la tabla? Escribe la letra que corresponda en cada caso: aleatoria (A), rectilínea (R) , circular (C), parábólica (P).
| Un ascensor que sube desde el bajo a la 4ª planta |
|
| Una mosca que vuela por la habitación. |
|
| Un satélite dando la vueta alrededor de laTierra | |
| Una pelota de baloncesto cuando se lanza un triple | |
| El extremo de las manecillas del reloj |
Cuando vamos a estudiar un movimiento, además de la trayectoria lo que nos interesa es conocer dónde se encuentra el móvil (el cuerpo que se mueve) en cada momento, para poder calcular qué distancias recorre y en cuanto tiempo lo hace.
Para eso necesitamos expresar matemáticamente dónde está el cuerpo, su posición. Y para hacer esto necesitamos elegir el sistema de referencia. Conocer la trayectoria nos va a permitir hacerlo; vamos a situar sobre la trayectoria el sistema de referencia para estudiar el movimiento.
Para ello tendremos que hacer dos cosas:
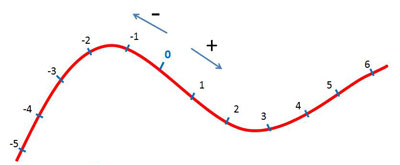
- Elegir un punto de la trayectoria como origen del sistema de referencia. Este punto será la posición 0.
- Para indicar a qué lado del origen está el cuerpo se emplean los signos + y -. En general se considera positiva la posición cuando se aleja del S. R. hacia arriba o hacia la derecha y negativo en caso contrario.
Haciendo clic en la imagen puedes ver paso a paso cómo se hace.
Una vez establecido el sistema de referencia, para indicar la posición del móvil, basta decir la distancia que lo separa del origen (signo incluído).
Al lugar que ocupa el cuerpo sobre la trayectoria, respecto del sistema de referencia, en cada momento, se le llama posición.
Por ejemplo
En la figura se muestra la trayectoria que están describiendo tres bolas (las tres describen la misma). Las distancias se miden en metros.
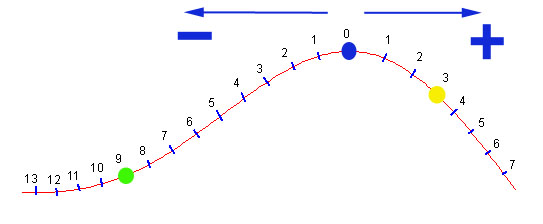
El el momento que muestra la imagen, las posiciones que ocupan son:
- La bola verde está en la posición - 9 m.
- La bola azul está en la posición 0 m (está en el origen del S.R.)
- La bola amarilla está en la posición 3 m.
La posición se suele representar mediante la letra “e” y, como ya sabes, en el Sistema Internacional se mide en metros (porque, al fin y al cabo, no es más que la distancia hasta el origen del sistema de referencia, una longitud).
Cuando un cuerpo se mueve, cambia de posición a lo largo del tiempo. Si un cuerpo ocupa en un instante determinado ti (instante inicial) una posición determinada ei (posición inicial), y cierto tiempo después, en otro instante tf (instante final) ocupa otra posición ef (posición final), entonces podremos decir que el cuerpo se ha movido. ¿Lógico, no?
Al tiempo que ha pasado entre ti y tf se le suele llamar tiempo transcurrido. Se calcula muy fácil: restando los dos tiempos, tf - ti (siempre el final menos el inicial, claro). Para representarlo se suele emplear el símbolo 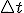 :
:
![]()
Durante ese tiempo el móvil habrá recorrido cierta distancia sobre la trayectoria, y habrá efectuado cierto desplazamiento 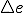 .
.
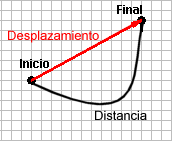
Llamamos desplazamiento a la diferencia entre dos posiciones determinadas, es decir la posición final menos la inicial.
![]()
Mucho cuidado…
El desplazamiento no es lo mismo que la distancia recorrida. Entre ellos hay varias diferencias importantes:
La distancia recorrida siempre es positiva, pero el desplazamiento puede ser positivo o negativo.
La distancia se recorre sobre la trayectoria. El desplazamiento no tiene nada que ver con la trayectoria, solo con las posiciones inicial y final; dos cuerpos pueden hacer el mismo deslazamiento por trayectorias diferentes y recorriendo distancias diferentes.
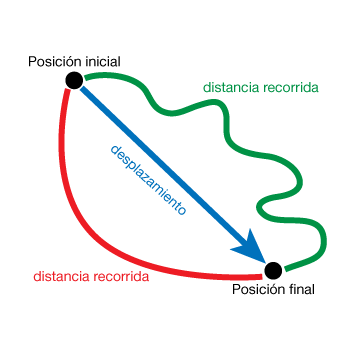
Observa esas diferencias en el siguiente enlace: Desplazamiento y distancia recorrida.En la imagen puedes ver cómo dos móviles que describe trayectorias diferentes (verde y roja) y recorren distancias distintas, efectúan, sin embargo, el mismo desplazamiento, el mismo cambio de posición.
Como ves, normalmente desplazamiento y distancia recorrida no coinciden. Pero...
Cuando la trayectoria es rectilínea y el movimiento no cambia de sentido, el desplazamiento coincide con la distancia recorrida, pero con signo.
Autoevaluación
Vamos a ver lo bien que has entendido la diferecia entre posición, desplazamiento y distancia recorrida...
1. Observa la siguiente trayectoria, en la que la distancia entre un cono y otro es de 40 m y está marcado el origen del S.R.

-
Escribe cuál sería la posición de cada cono de izquierda a derecha (ten cuidado con el signo):
- - - - 0 - - - - -
-
Si un ciclista comienza a moverse desde la posición –160 m, hacia la derecha, y tarda 20 segundos en ir de cono a cono, completa la siguiente tabla en la que se recoge el instante de tiempo en el que se encuentra en las diferentes posiciones.
Posición (m) Tiempo (s) -160 0 -120 -80 -40 0 40 80 120 160 200
2. Observa la siguiente trayectoria. Ahora, la distancia entre un cono y otro es de 100 m y el banderín señala el origen del sistema de referencia.

-
Escribe cuál sería la posición de cada cono de izquierda a derecha (ten cuidado con el signo):
- - - - - 0 - - - - - - - -
-
Si una persona comienza a caminar en la posición 600 m, hacia la izquierda, y tarda 5 minutos en ir de cono a cono, completa la siguiente tabla, en la que se asocia a cada instante de tiempo la posición que ocupa la persona:
Tiempo (min) Posición (m) 0 5 10 15 20 25 30 0 35 40 45 50
|
En el primero, ya que la velocidad es siempre la misma.
| |
|
En el segundo, ya que la trayectoria está bien definida.
| |
|
En el primero, ya que la trayectoria es rectilínea.
|
4. Observa la siguiente tabla de datos relativos al movimiento de una bola lanzada sobre una superficie horizontal lisa.
| Posición (m) | Tiempo (s) |
| 20 | 10 |
| 25 | 20 |
| 30 | 30 |
| 35 | 40 |
| 40 | 50 |
| 45 | 60 |
| 50 | 70 |
| 55 | 80 |
| 60 | 90 |
| 65 | 100 |
| 70 | 110 |
a) ¿En qué instante está la bola en la posición 50 m?
|
En el instante t = 10 s.
| |
|
en el instante t = 55 s.
| |
|
En el instante t = 70 s
|
|
10 s
| |
|
70 s
| |
|
100 s
|
5. Observa el siguiente movimiento:
a) ¿Cuál es la posición inicial de la bola?
|
0 m
| |
|
- 30 m
| |
|
30 m
|
|
6 s
| |
|
9 s
| |
|
30 s
|
|
12 s
| |
|
3 s
|