3.- ¿Vamos rápido o veloces?
¿Qué tal va la cosa? Seguro que muy bien ¿no? O... ¿Tal vez vamos como las balas...?

Imagen: morguefile
En los dos primeros apartados del tema has aprendido algunas cosas sobre los movimientos, en las que probablemente no habías pensado nunca. Es absolutamente normal. Ideas como sistema de referencia, trayectoria y posición las tenemos todos y todas muy asumidas, forman parte de nuestra experiencia cotidiana y no solemos reparar en ellas.
Pero hay otras palabras que a todo el mundo se le vienen a la cabeza cuando piensa en el movimiento, y de las que aún no hemos hablado... Nos referimos a palabras como "rápido", "despacio" o "velocidad". Son palabras que todo el mundo usa, pero... ¿sabemos lo que son? ¿Sabrías calcular lo rápido que se ha movido un coche? ¿Estamos hablando de la misma cosa cuando decimos "rapidez" y cuando decimos "velocidad"?
En este apartado vas a encontrar respuesta a estas preguntas...
Vamos a empezar con la rapidez. Bueno, la cosa es muy sencilla; en realidad, aunque no la hemos nombrado, ya has hecho algún ejercicio de autoevaluación en el que tenías que usar el concepto de rapidez:
La rapideznos dice la relación que hay entre la distancia que recorre un cuerpo y el tiempo que tarda en recorrerla

Su unidad en el Sistema Internacional es el m/s.
Sencillo ¿verdad? Veamos algunos ejemplos:
-

¿Con qué rapidez se mueve el ciclista del primer ejercicio de la autoevaluación del apartado anterior?
Nos dice el enunciado que el ciclista tarda 20 s en ir de cono a cono. Por otro lado, también nos dice que la distancia entre cono y cono es de 40 m. Por tanto, el ciclista recorre 40 m cada 20 s, por lo que su rapidez será:
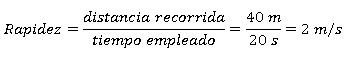
-
¿Con qué rapidez se mueve la bola del último ejercicio de la autoevaluación del apartado anterior?
En este caso, la distancia entre marcas es de 10 m, y la bola tarda solo 3 s en recorrerlos. Por tanto, la rapidez de la bola será:

-

Imagen: flickr.com / Fiat Yamaha Team
¿Qué rapidez llevará una moto de GP que completa una vuelta a un circuito de 4268 m en tan solo 1 minuto y 12 segundos?
La distancia que recorre la moto es la longitud del circuito, 4268 m. El tiempo que tarda en hacerlo es 1 min y 12 segundos, pero no podemos emplearlo así, sino que lo tenemos que expresar en segundos.Como 1 minuto tiene 60 s, en total el tiempo empleado por la moto ha sido de 72 s (60 + 12 = 72).
La rapidez que ha llevado será:
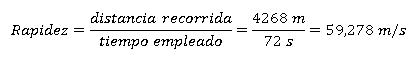
En nuestro lenguaje cotidiano no distinguimos entre velocidad y rapidez. Pero los científicos, que son tan quisquillosos, sí que necesitan diferenciarlas. Y es que, en realidad, no son la misma cosa, aunque sí se parezcan un poco.
La velocidad nos dice la relación que hay entre el desplazamiento efectuado por un móvil y el tiempo que tarda en realizarlo

Su unidad en el Sistema Internacional es el m/s
Para calcular la rapidez empleamos la distancia recorrida por el móvil, pero para calcular la velocidad empleamos el desplazamiento efectuado por el móvil. Recuerda que distancia recorrida y desplazamiento no son la misma cosa, de manera que rapidez y velocidad tampoco lo serán.
Solo en el caso de movimientos rectilíneos en los que el móvil no cambie de sentido, la velocidad y la rapidez coinciden ya que en estos casos coincide la distancia recorrida y el desplazamiento efectuado.
Veamos también algunos ejemplos:

-
¿Con qué velocidad se ha movido el ciclista del primer ejercicio de la autoevaluación del apartado anterior entre los instantes ti = 40 s y tf = 100 s?
Para calcularla solo tenemos que fijarnos en las posiciones que el ciclista ha ocupado en esos instantes. Estas posiciones las podemos ver en la tabla que habrás completado en el ejercicio:
En ti = 40 s, la posición del ciclista era ei = - 80 m
En tf = 100 s, la posición del ciclista era ef = 40 m
Con estos datos podremos calcular el desplazamiento efectuado por el ciclista y la velocidad que ha llevado:
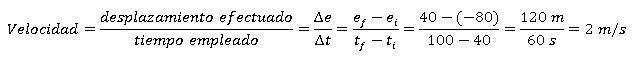
-
¿Con qué velocidad se ha movido la persona del segundo ejercicio de la autoevaluación del apartado anterior entre los instantes ti = 15 min y tf = 35 min?
Procedemos como en el ejemplo anterior. Primero tenemos que saber las posiciones que, en esos instantes, ha ocupado la persona. Lo miramos en la tabla que habrás completado:
En ti = 15 min, la posición de la persona era ei = 300 m
En tf = 35 min, la posición de la persona era ef = - 100 m
Por otro lado, tenemos que tener en cuenta en este ejercicio es que los tiempos no están en las unidades adecuadas. Están en minutos, pero nosotros los necesitamos en segundos. Como en realidad no nos interesan ni ti ni tf, sino su diferencia,
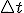 , es esa diferencia la que pasaremos a segundos:
, es esa diferencia la que pasaremos a segundos:
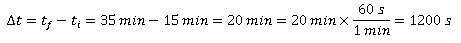
Y ahora podemos ya calcular la velocidad de la persona:
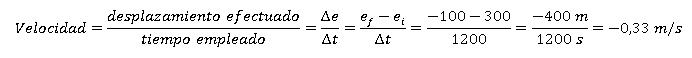
Observa que la velocidad es en este caso negativa, ya que la persona se mueve hacia la parte negativa del S.R. (en este caso, hacia la izquierda)
Recuerda…
La velocidad nos da más información que la rapidez:
- La rapidez solo nos dice "lo deprisa" que se mueve un cuerpo. Es siempre positiva, porque la distancia recorrida siempre es positiva.
- La velocidad nos dice, además, hacia dónde se mueve. De eso se encarga su signo:
- Es positiva si el móvil se desplaza en el sentido positivo del sistema de referencia.
- Es negativa si el móvil se desplaza en el sentido negativo del sistema de referencia.
Autoevaluación
Hemos estado observando el movimiento de una hormiga y anotado las posiciones que ha ido ocupando en diferentes instantes de tiempo. Hemos visto que cuando nuestro cronómetro marcaba el instante ti = 5 s, se encontraba en la posición ei = 15 cm; y cuando el cronómetro marcaba el instante tf = 12 s, la posición que ocupaba era ef = 8 cm.
1. ¿Cuál es la velocidad de la hormiga que estamos observando?
|
1 m/s
| |
|
0,01 m/s
| |
|
- 0,01 m/s
| |
|
- 1 m/s
|
|
1 m/s
| |
|
0,01 m/s
| |
|
- 0,01 m/s
|
3. Hemos dejado caer una pelota desde un acantilado y estudiamos su movimiento con el sistema de referencia que ves en la imagen. ¿Cómo será la velocidad de la pelota en ese sistema de referencia?
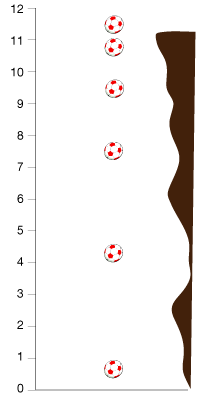
|
Positiva, como su rapidez.
| |
|
Negativa, como su rapidez.
| |
|
Negativa, justo al contrario que su rapidez
|
Has visto en los ejemplos y en los ejercicios de autoevaluación que es muy importante usar siempre las unidades adecuadas. En el caso de la velocidad y de la rapidez la unidad adecuada, la del Sistema Internacional, es el metro partido por segundo (m/s).
Pero seguro que te suenan mucho más las velocidades expresadas en otras unidades, sobre todo en "kilómetros por hora" (km/h) ¿no? que es la unidad más habitual cuando hablamos de la rapidez o la velocidad de un vehículo, por ejemplo.
Por eso es muy importante saber cambiar de m/s a km/h y viceversa, ya que en cualquier problema de cinemática (de movimientos) debemos tener cuidado de que estemos correctas las unidades. En cualquier cambio de unidades donde tengamos a la vez más de una unidad: m/s, kg/m3, etc., lo único que tenemos que hacer es cambiar por separado cada una de las unidades y realizar las operaciones que nos salgan.
Por ejemplo
Para pasar 54 km/h a m/s, lo que tenemos que hacer es pasar los 72 km a m y 1 h a segundos:
54 km = 54.000 m
1 h =3.600 s
Luego realizamos las operaciones habituales para calcular la rapidez o la velocidad, es decir, dividir distancias entre tiempos:
![]()
Seguro que se te ha quedado claro, pero por si acaso, no te vendría mal echar un vistazo a este enlace:
Autoevaluación
1. Pasa a m/s las siguientes velocidades y marca las respuestas adecuadas
a) 57 km/h
|
15,83 m/s
| |
|
205,2 m/s
|
|
468 m/s
| |
|
36,1 m/s
|
a) 90 m/s
|
324 km/h
| |
|
25 km/h
|
|
72 km/h
| |
|
5,56 km/h
|
3. Si te apetece seguir practicando el cambio de km/h a m/s y quieres, de paso, conocer las velocidades típicas de algunos movimientos, completa la tabla poniendo la velocidad en m/s.
ASÍ DE RÁPIDO SE MUEVEN ALGUNAS COSAS...
| Movimiento | Velocidad (m/s) | Velocidad (km/h) |
| Caracol | 0,00054 | |
| Hormiga andando | 0,036 | |
| Tortuga | 0,072 | |
| Persona andando | 4,68 | |
| Hombre corriendo | 14,4 | |
| Liebre | 36 | |
| Atletas 100 m | 43,2 | |
| Guepardo | 104,4 | |
| Pájaro en vuelo | 158,4 | |
| Automóvil comercial | 187,2 | |
| Avión de pasajeros | 792 | |
| Sonido en el aire | 1224 | |
| Reactor de reconocimiento | 3.312 | |
| Tierra alrededor del Sol | 106.560 | |
| Luz (ondas electromagnéticas) en el vacío | 1.080.000.000 |
Esta última velocidad, la de las ondas electromagnéticas en el vacío, es la más alta que se puede alcanzar y solo pueden alcanzarla precisamente ellas.