EL MOVIMIENTO UNIFORME

• El movimiento uniforme es aquel cuya rapidez es constante, es siempre la misma.

  • Si además, también la dirección del movimiento y su sentido son siempre los mismos, el movimiento será rectilíneo y uniforme (MRU).
  • En un MRU no solo es constante la rapidez, sino también la velocidad.
  • La característica más destacada de un movimiento uniforme es que el móvil recorre distancias iguales en tiempos iguales.

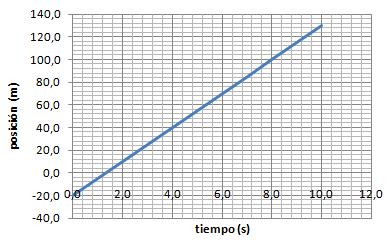
• La gráfica más importante de un MRU es la gráfica posición-tiempo (e-t). Siempre es una recta y de ella podemos obtener las constantes del movimiento:

  • El punto donde la recta corta al eje "e" nos indica la posición inicial del móvil (posición cuando t=0)
  • La pendiente (constante) de la recta nos indica la velocidad del móvil.

• La ecuación más importante y útil del MRU es la ecuación de posición, que nos permite calcular la posición del móvil en cualquier instante.

  

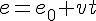
  La representación gráfica de esta ecuación es la gráfica e-t del movimiento.

---

EL MOVIMIENTO UNIFORMEMENTE ACELERADO

• El movimiento uniformemente acelerado es aquel cuya aceleración es constante, es siempre la misma.

  • Si, además, la trayectoria es una linea recta, se tratará de un movmiento rectilíneo uniformemente acelerado (MRUA).

  • La aceleración nos indica cómo de rápido varía la velocidad de un cuerpo.

  • Las características más destacadas de un MRUA son:

    • La velocidad varía siempre del mismo modo, al mismo ritmo, ya sea aumentando la rapidez o disminuyéndola (frenando)
    • El móvil no recorre distancias iguales en tiempos iguales.

• En el MRUA hay dos gráficas importantes:

  

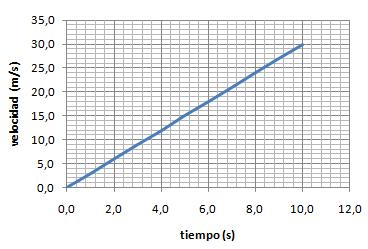
  • La gráfica velocidad-tiempo (v-t), que es siempre una recta, de la que podemos obtener algunas de las constantes del movimiento:

    • El punto donde la recta corta al eje "v" nos indica la velocidad inicial del móvil (velocidad cuando t=0)
    • La pendiente (constante) de la recta nos indica la aceleración del móvil.

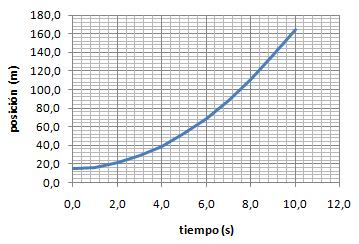
  • La gráfica posición-tiempo (e-t), que es siempre una parábola, de la que podemos obtener la otra constante del movimiento.

    • El punto donde la parábola corta al eje e nos indica la posición inicial del móvil (posición cuando t=0)

• Para describir el MRUA necesitamos dos ecuaciones de movimiento:

  • La ecuación de la velocidad, cuya representación gráfica es la gráfica v-t

    

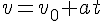
  • La ecuación de la posición, cuya representación gráfica es la gráfica e-t

    

---

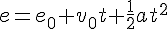
RESOLUCIÓN DE PROBLEMAS DE MOVIMIENTO

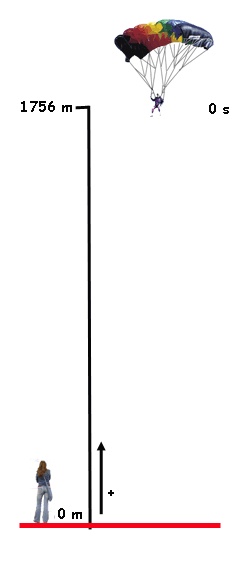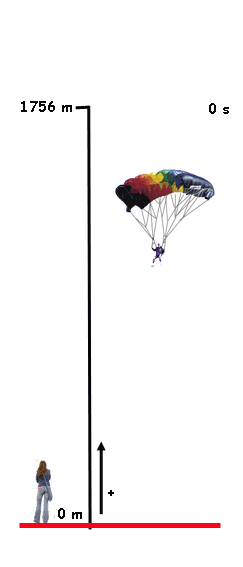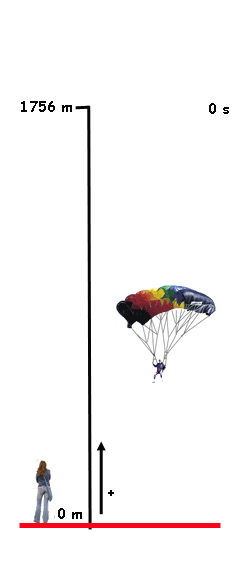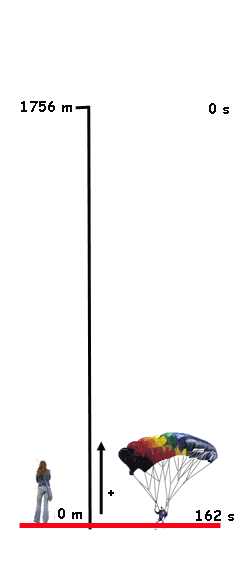
• Para resolver problemas de movimiento resulta siempre muy útil seguir un procedimiento riguroso y ordenado:

  1. Leer el enunciado atentamente y hacer un esquema gráfico de la situación que te ayude a comprenderlo bien.
  2. Establecer el sistema de referencia que vas a utilizar (dónde está el origen y cuál es el sentido positivo).
  3. Escribir el valor de las constantes del movimiento.
  4. Establecer la ecuación del movimiento (aunque la tengas incompleta).
  5. Reflexionar sobre qué magnitud tienes que calcular y qué datos vas a necesitar.
  6. Sustituir en la ecuación de movimiento los datos necesarios (mucho ojo con las unidades).
  7. Resolver la ecuación que obtengas.
  8. Dar la solución, respondiendo a la pregunta del problema.

• Las ecuaciones que puedes encontrarte en los problemas de movimiento pueden ser de tres tipos:

  • Ecuaciones de primer grado con una incógnita: Se resuelven transponiendo términos y despejando la incógnita.

  • Sistemas de ecuaciones de primer grado con una incógnita: Se pueden resolver gráficamente o por cualquiera de los tres métodos analíticos (sustitución, igualación o reducción)<

    /li>

  • Ecuaciones de segundo grado con una incógnita, cuya forma general es 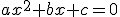(con 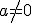): Se resuelven empleando la fórmula 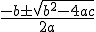, que puede aplicarse incluso cuando la ecuación está incompleta.