1.3.- Ahora las "fórmulas"
Bueno... pues ya has aprendido cómo son las gráficas e-t y v-t de un movimiento uniforme.
(Recuerda que no es necesario que sea rectilíneo; esas gráficas son válidas para cualquier movimiento uniforme, siempre que hayamos establecido un sistema de referencia adecuado sobre la trayectoria)
La verdad es que solo con la gráfica e-t ya podemos extraer toda la información importante sobre el movimiento:
- La posición inicial (e0), que es el punto donde la gráfica corta al eje de ordenadas.
- La velocidad constante del movimiento (v), que es la pendiente de la recta que nos sale.
Pre-conocimiento
Pongamos cada cosa en su sitio…
No cabe duda de que la gráfica e-t es muy útil (y muy fácil, ¿verdad?). Pero no creas que nos soluciona todo lo queramos saber sobre estos movimientos; tiene sus cosillas. Sobre todo que, para hacerla, es necesario conocer las constantes del movimiento o tener ya una tabla de datos de posiciones ocupadas en diferentes instantes.
Aunque por lo general siempre conoceremos la posición inicial (puesto que la elegimos nosotros normalmente), no siempre conocemos de antemano la velocidad del móvil.
Incluso teniendo las constantes del movimiento, para hacer la gráfica necesitamos hacer antes la tabla de datos... ¿y cómo la hacemos? ¿cómo sabemos, de antemano, qué posición ocupará el móvil en cada instante de tiempo? ¿Tendríamos que medirla? ¿Tendríamos que calcularla? Si es así... ¿cómo lo hacemos? (Piensa en ello ¿Cómo "aparecen" como por arte de magia los datos en la hoja de cálculo que has usado para experimentar con las gráficas?)
En fin... que la gráfica es un poquito engorrosa de hacer. Pero ¡eso no es todo! Se nos pueden plantear preguntas que puede ser complicado resolver empleando la gráfica... incluso si ya la tenemos.
Caso de estudio
Por ejemplo…
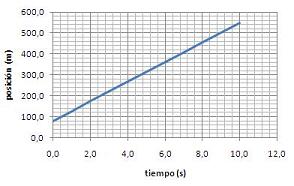
Imagina el movimiento uniforme de un tren que tiene que hacer un viaje muy, muy largo, por una vía que le permite moverse con velocidad constante de 47 m/s . Supón que en el sistema de referencia que un viajero ha elegido para estudiar el movimiento del tren, la posición inicial es... digamos... que 80 m.
¿Podrías construir la gráfica e-t de este movimiento? Seguro que sí, que lo harías sin problema y que obtendrías algo así como lo que ves en la imagen.
Ahora... con esa gráfica ya hecha y a la vista...
¿Me podrías decir cuánto tiempo debe pasar para que el tren se encuentre en la posición...89653,76 m? O, por ejemplo, ¿Podrías decir en qué posición se encontrará el tren en el instante 723 s?
Bueno, no cabe duda de que responder a las preguntas anteriores usando la gráfica... es posible, pero bastante trabajoso. Por no decir que la gráfica debe estar perfectamente hecha para que las respuestas sean correctas.
Entonces... ¿cómo podríamos responder a este tipo de preguntas de una forma "fácil"?
Pues, afortunadamente, como en casi todos los casos sucede en la Ciencia, las Matemáticas vienen en nuestra ayuda.
Pre-conocimiento
¿Recuerdas que en el Tema 1 de este bloque viste una presentación donde te hablábamos de cómo hacer gráficas?
En esa presentación aparecía una gráfica idéntica a la gráfica e-t de un movimiento uniforme. Sería conveniente que volvieras a ver la presentación... solo tienes que hacer clic en la imagen.
Presta especial atención a la parte donde habla de la función afín.
Si has mirado con atención la presentación anterior, no te costará ningún trabajo entender que...
Actividad
La gráfica e-t de un movimiento uniforme es la representación de una función afín, cuya expresión matemática (cuya fórmula) tiene la forma:
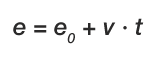
A esta fórmula se la conoce como ecuación del movimiento rectilíneo uniforme
¡Es muy fácil! ¿verdad? Pero para que lo tengas ya claro del todo, observa en la siguiente animación la relación que existe entre la gráfica e-t y la ecuación de un movimiento uniforme:
Caso de estudio
Ahora sí…
Imagen: flickr.com / Ventura2
Usando la ecuación del movimiento sí que es fácil responder a las preguntas que antes, con la gráfica, resultaba bastante latoso. Observa:
Si lees con atención la situación que nos planteábamos, te darás cuenta de que las constantes del movimiento (recuerda, la velocidad y la posición inicial del tren) son
e0 = 80 m
v = 47 m/s
Por lo tanto, la ecuación que describe este movimiento concreto será: e = 80 + 47·t
¿Cómo podríamos calcular ahora la posición del tren en el instante 723s?... Pues verás qué fácil: Solo tenemos que sustituir en la ecuación de movimiento del tren, la "t" (que representa al tiempo) por ese valor concreto (723 s) y hacer la cuenta:
e = 80 + 47·723 = 80 + 33981 = 34061
de manera que a los 723 s el tren se encontrará en la posición 34061 m
¡Ves qué fácil ha sido!
¿Y la otra pregunta? ¿Será también tan fácil de contestar?... Creo que sospechas que sí... vamos a verlo.
Queríamos saber en que instante se encontrará el tren en la posición 89653,76 m ¿recuerdas? Pues bien, solo tenemos que sustituir la "e" de la ecuación (que representa la posición del tren) por ese valor (89653,79 m) y hacer las cuentas. Aunque en este caso las cuentas son algo más complicadas, porque hay que despejar el tiempo, la "t", que es ahora la incógnita que buscamos. Observa con atención cómo se hace:
| 1 | Sustituimos en la ecuación los valores: | 89653,76 = 80 + 47 · t |
| 2 | El 80, que está sumando en el segundo miembro (a la derecha del signo igual) lo pasamos al primer miembro (a la izquierda del signo igual) pero sumando: | 89653,76 – 80 = 47 · t |
| 3 | Hacemos la cuenta del primer miembro (la resta que hay): | 89573,76 = 47 · t |
| 4 | Pasamos el 47 que multiplica a la "t" en el segundo miembro, al primer miembro, pero dividiendo: | 89573,76 ÷ 47 = t |
| 5 | Hacemos la cuenta de dividir... y ya sabremos el valor de la incógnita, de la "t", lo que buscamos: | t = 1905,82 |
Por lo tanto, el tren estará en la posición 89653,76 m en el instante 1905,82 s (unos 31 minutos y 46 s después de salir)
Usando la gráfica... seguro que no hubieses podido responder. En el siguiente apartado vas a ver unos ejemplos más de cómo usar la ecuación de un movimiento uniforme. Estudia con atención todos los ejemplos.
Pregunta de Elección MúltipleAutoevaluación
1. ¿Qué podrías decir de un movimiento rectilíneo uniforme cuya ecuación de movimiento fuese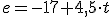 
? Señala las respuestas que consideres correctas. El sistema de referencia que se ha usado para establecer esa ecuación ha sido éste:
|
Al iniciar el movimiento, el cuerpo se encuentra a la izquierda del origen del sistema de referencia.
| |
|
El objeto se mueve con una velocidad, constante, de 17 m/s
| |
|
El cuerpo se mueve, hacia la izquierda, con una velocidad constante de 4,5 m/s
|
Uy, uy... mira con atención la ecuación ¡y el sistema de referencia!
¡Estupendo! ¡Parece que te has enterado muy bien!
Actividad de Espacios en Blanco
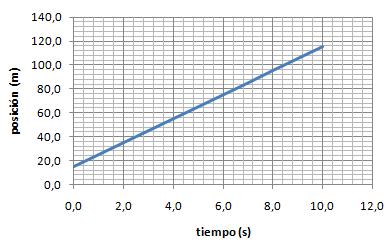
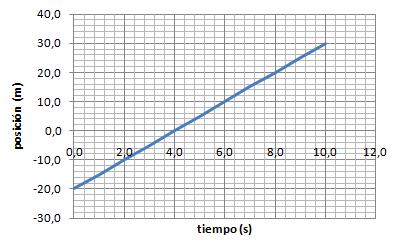
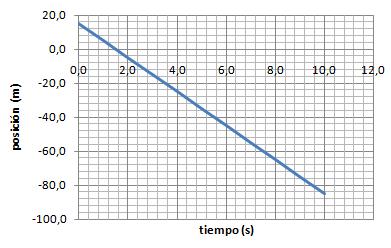
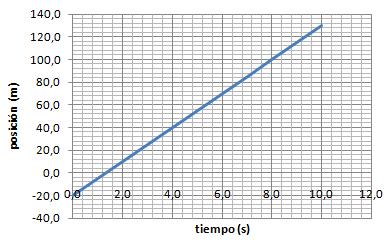
2. Observa con atención las siguientes gráficas. Todas representan movimientos uniformes...
 |
 |
| Gráfica nº 1 |
Gráfica nº 2 |
 |
 |
| Gráfica nº 3 |
Gráfica nº 4 |
Esas gráficas corresponden a las siguientes ecuaciones de movimiento:
 |
 |
 |
 |
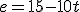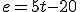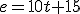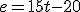| Ecuación A |
Ecuación B |
Ecuación C |
Ecuación D |
Haz corresponder cada una de las gráficas con la ecuación a la que representa...
| Gráfica | Ecuación |
| 1 | |
| 2 | |
| 3 | |
| 4 |