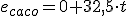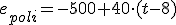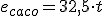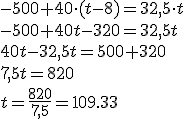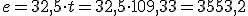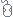Aplicamos la ecuación del MRU

Imagen: Wikimedia commons
El récord de la hora
El 19 de julio de 2005 el ciclista checo Andrei Sosenka estableció el récord de la hora moviéndose a una velocidad de unos 13,8 m/s. Este récord mide la distancia que un ciclista es capaz de recorrer en una hora bajo unas condiciones determinadas (establecidas por al UCI, la Unión Ciclista Internacional).
¿En cuánto estableció Andrei el récord de la hora? (Es decir, ¿qué distancia recorrió en una hora si se movía a la velocidad de 13,8 m/s?)

Imagen: Wikimedia commons
¿Alguna vez has saltado en paracaídas?
Debe ser una experiencia alucinante ¿no crees? En un salto en paracaídas, desde que éste se abre hasta que el paracaidista llega al suelo, el movimiento que lleva es prácticamente uniforme. No cae cada vez más rápido porque el rozamiento con el aire lo impide (como verás en el siguiente tema...)
La cuestión es que Belén es una enamorada de Juanmi... bueno, de un tipo que salta en paracaídas. Su novio le ha comentado que en su último salto abrió su paracaídas a una altura de 1756 m (según indicaba su altímetro). Belén pensó... "justo el dato que necesitaba" y le dijo a su novio que iba a calcular la velocidad con la que cayó.
- ¿Cómo? -le contestó Juanmi sin creérselo-
- Mientras saltabas he cronometrado el tiempo que tardabas en caer... je, je; han sido 2 minutos y 42 s. Lo demás es... pura Física.
¿Sabrías tú, como Belén, calcular la velocidad a la que ha caído Juanmi con su paracaídas?
En el ejemplo anterior ha habido que resolver una sencilla ecuación de primer grado con una incógnita. Esto es algo habitual en la Ciencia y la Tecnología; sin las Matemáticas se quedarían sin su herramienta más preciada. Si no fuera por ellas, por las Matemáticas, no hubiera sido posible el espectacular desarrollo que la Ciencia y la Tecnología ha experimentado en los últimos siglos.
Eso de las "ecuaciones" es algo que "da mucho miedo" ¿verdad? Pero lo cierto es que no son nada difíciles; resolverlas es... casi un entretenido pasatiempo. Te sugerimos que no dejes de visitar el siguiente enlace. En él podrás aprender muchas cosas sobre las ecuaciones de primer grado con una incógnita y practicar... ¡hasta que te hartes!
Rápido como el rayo…
La verdad es que en la Naturaleza es difícil encontrar movimientos rectilíneos uniformes que duren mucho tiempo.
Sí que hay movimientos uniformes, y muy importantes, que duran y duran (y esperemos que así siga siendo). Hablamos de, por ejemplo, el movimiento de los planetas alrededor del Sol o de los satélites alrededor de los planetas. Por ejemplo, en su movimiento alrededor del Sol, la Tierra va siempre igual de rápido ¡Todos los años duran lo mismo!. De modo que su movimiento es uniforme (aunque no sea rectilineo)
Pero sí que podemos encontrar algunos movimientos muy importantes y que sí que son rectilíneos y uniformes. Claro, que se trata de movimientos de "cuerpos" un poco "raros". La luz, por ejemplo, es uno de esos casos.
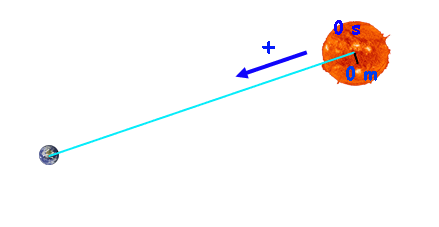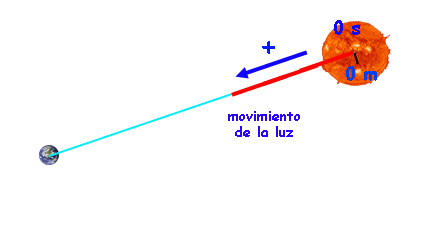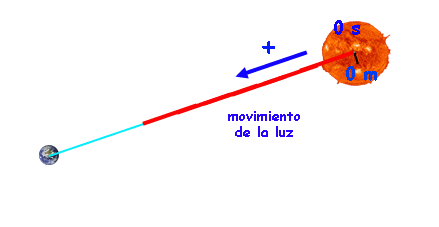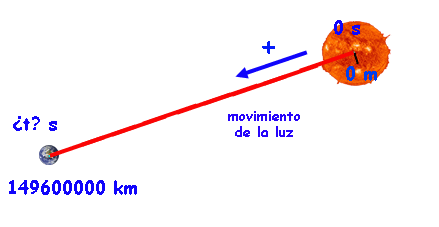
La luz se mueve, en el vacío y en el aire, en línea recta y con una velocidad constante de ¡¡300.000 km/s!!
La más grande que existe. Nada se mueve tan rápido como la luz. Pero claro, por rápido que se mueva, si tiene que recorrer distancias muy grandes... pues tarda su tiempo, no te creas.
Por ejemplo, el Sol está de la Tierra a unos... 149.600.000 km (un "puñao de lejos") ¿Cuánto tardará la luz del Sol en llegar hasta la Tierra?
¿Te vas "quedando con la copla"?
Para resolver con orden un problema de movimiento uniforme, tendrás que:
- Leer el enunciado atentamente y hacer un esquema gráfico de la situación que te ayude a comprenderlo bien.
- Establecer el sistema de referencia que vas a utilizar (dónde está el origen y cuál es el sentido positivo).
- Escribir el valor de las constantes del movimiento: e0 y v.
- Establecer la ecuación del movimiento (aunque la tengas incompleta).
- Reflexionar sobre qué magnitud tienes que calcular y qué datos vas a necesitar.
- Sustituir en la ecuación de movimiento los datos necesarios (mucho ojo con las unidades).
- Resolver la ecuación de primer grado que obtienes.
- Dar la solución, respondiendo a la pregunta del problema.

Imagen: dreamstime
¿Lo pillará o no lo pillará?
¿A que es raro ver una peli de polis en la que no haya una persecución? Ya sea en coche (lo más tradicional) o en moto, camión... o cualquier tipo de vehículo (incluso nave espacial), las escenas en las que el poli persigue a toda velocidad al malhechor nunca faltan.
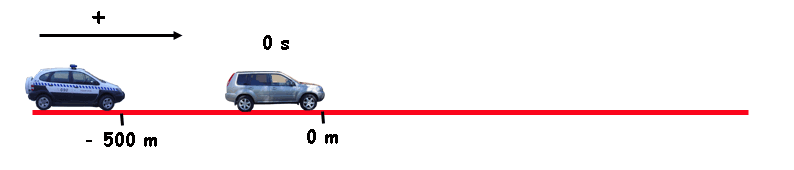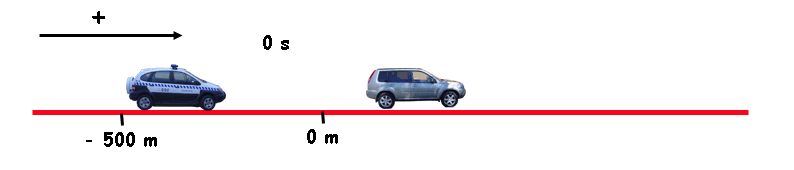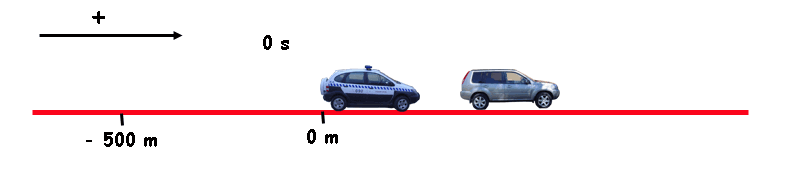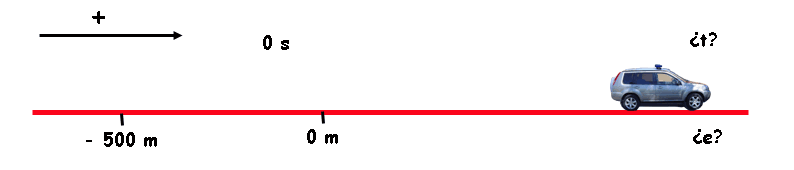
Imagina... El policía ve, 500 m más adelante, que un ladrón monta en su coche y sale huyendo a toda velocidad. Ocho segundos más tarde el poli se pone en marcha tras el ladrón.
Supongamos que ambos se van a mover con movimiento uniforme; el ladrón a 117 km/h y el poli a 144 km/h (deberá ir un poco más rápido que el ladrón si queremos que todo termine bien) .
Está claro que lo pillará ¿verdad? Pero... ¿Dónde? ¿Cuándo?
Este tipo de situaciones son "un poquito" más complicadas que las que has visto en los ejemplos anteriores de aplicación de las ecuaciones de movimiento. Pero "se atacan" igual.
La diferencia es que ahora tienes que manejar a la vez dos ecuaciones de movimiento. Antes de seguir te será muy, muy útil que eches un vistazo atento a estos dos enlaces. No te asustes por el nombre... enseguida entenderás por que te van a ser muy útiles:
Para saber más…
…sobre sistemas de ecuaciones y cómo se resuelven, puedes visitar los siguientes enlaces. Aprenderás más métodos para resolverlos, verás que algunos sistemas son… un poco "raros" y podrás practicar "hasta que te hartes":

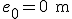
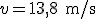
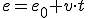 , en el caso de nuestro ciclista, y teniendo en cuenta lo que valen las constantes del movimiento, la ecuación será:
, en el caso de nuestro ciclista, y teniendo en cuenta lo que valen las constantes del movimiento, la ecuación será:
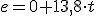
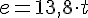
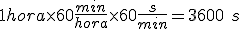 , y sustituimos en la ecuación de movimiento:
, y sustituimos en la ecuación de movimiento:
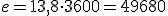
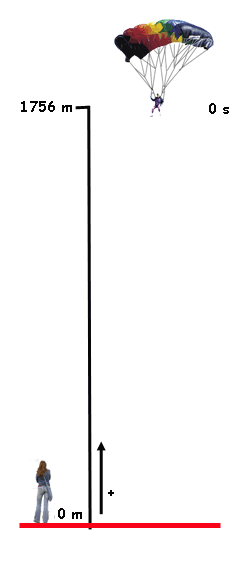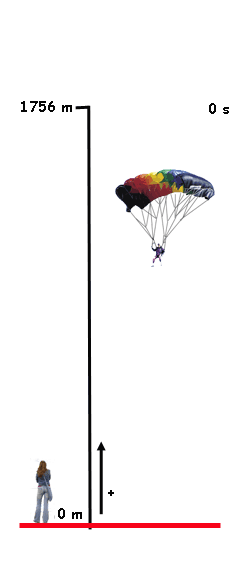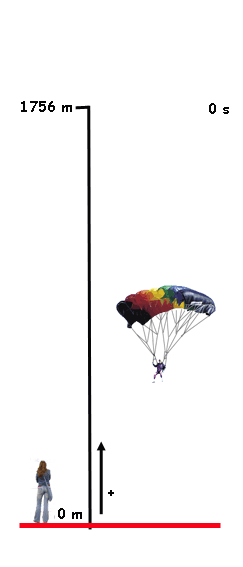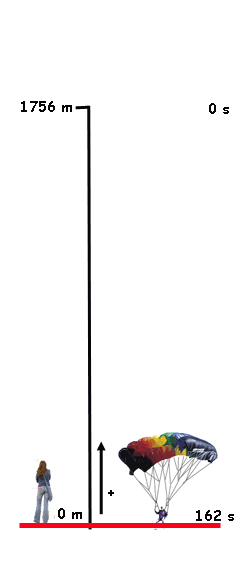
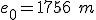
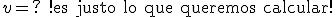
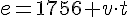
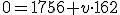
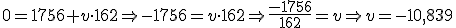
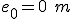
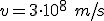 (la velocidad de la luz, pero expresada en las unidades del SI: 300.000 km/s = 300.000.000 m/s)
(la velocidad de la luz, pero expresada en las unidades del SI: 300.000 km/s = 300.000.000 m/s)
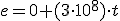 , que podemos escribir de modo más simple...
, que podemos escribir de modo más simple... 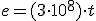
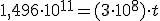
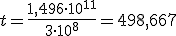
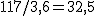 ;
; 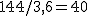 . Las constantes de cada movimiento serán...
. Las constantes de cada movimiento serán...
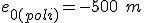
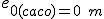
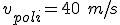
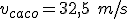
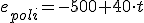 ;
;