5.4.1. Haciendo cálculos con la energía potencial gravitatoria
Antes de nada, recordemos la fórmula para calcular la energía potencial gravitatoria y las magnitudes que se emplean:
| MAGNITUDES IMPLICADAS | ||
| Magnitud | Unidad | Símbolo |
| energía potencial (EP) | julios | J |
| masa (m) | kilogramos | kg |
| altura (h) | metros | m |
Caso de estudio
Ejemplo 1
Una maceta de 2 kg de masa está situada a 3 metros de altura. ¿Qué energía potencial posee?
Para resolver este problema solo tenemos que sustituir los valores de las magnitudes masa y altura en la fórmula, en la unidad del SI y hacer el cálculo:
EP = 9,8 m/s2 · 2 kg · 3 m = 58,8 kg·m2/s2 = 58,8 J
Pre-conocimiento
Cambios de unidades…
Algunas veces necesitarás cambiar de unidades. De centímetros a metros, o de gramos a kilogramos, etc. Si no recuerdas bien cuáles son los múltiplos y submúltiplos más habituales de las unidades de medida, visita el siguiente enlace: Cambios de unidades.
En él puedes ver una animación que te recordará cuáles son múltiplos y submúltiplos de las unidades y también algunos ejemplos de cómo se pasa de unas unidades a otras.
Pregunta de Elección MúltipleAutoevaluación:
Un ascensor está a 20 m de altura con 3 toneladas de masa en su interior. ¿Qué energía potencial gravitatoria tendrá?
|
588 J.
| |
|
588000 J.
| |
|
60000 J.
|
Caso de estudio
Ejemplo 2
Una maceta situada a 3 metros de altura tiene una energía potencial de 44,1 julios, ¿cuál es su masa?
Sustituimos en la fórmula los valores de las magnitudes que conocemos (energía potencial y la altura):
44,1 J = 9,8 m/s2 · m · 3 m
Hacemos los cálculos que se puedan hacer. En este caso tan solo podemos multiplicar, en el segundo miembro de la igualdad, 9,8×3:
44,1 J = 29,4 m2/s2 · m
La magnitud que no conocemos, la masa, la tendremos que despejar de la fórmula. Para ello hay que dividir los dos miembros por el número que la acompaña (29.4). En resumen, lo que está multiplicando en un miembro "pasa" al otro dividiendo.
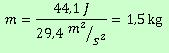
Aunque te parezca mentira, acabas de resolver una ecuación de primer grado. Puedes repasar en una presentación animada los pasos que has dado para hacerlo. Tan solo tienes que pulsar el siguiente enlace: Ecuaciones de primer grado.
Pregunta de Selección Múltiple
Autoevaluación:
1. Una manzana cuelga de la rama de un manzano situada a 4 metros del suelo, la energía potencial que posee es de 7,84 J. ¿Cuál es la masa de la manzana?
200 gramos.
| |
0,2 kg.
| |
307 gramos.
| |
| |
| |
| |
Caso de estudio
Ejemplo 3
Una maceta de 4 kg de masa, posee una energía potencial de 392 J, ¿a qué altura del suelo está situada?
Sustituimos en la fórmula los valores de las magnitudes que conocemos (la energía potencial y la masa):
392 J = 9,8 m/s2 · 4 kg · h
Hacemos los cálculos que se puedan hacer. En este caso tan solo podemos multiplicar, en el segundo miembro de la igualdad, 9,8×4:
392 J = 39,2 m ·kg/s2 · h
La magnitud que no conocemos, la altura, la tendremos que despejar de la fórmula. Para ello hay que dividir los dos miembros por el número que la acompaña (39.2). En resumen, lo que está multiplicando en un miembro "pasa" al otro dividiendo.
Pregunta de Elección Múltiple
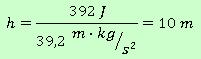
Autoevaluación:
1. Queremos que una piedra de 50 hg de peso adquiera una energía potencial de 490 J ¿cuántos metros de altura la debemos elevar?
|
10 metros.
| |
|
1 metro.
| |
|
9.8 metros.
|
Actividad de Espacios en Blanco
2. Rellena las celdas vacías que hay en la tabla siguiente. Presta mucha atención, porque para ello tendrás que cambiar algunas veces las unidades que aparecen a la que corresponda en el Sistema Internacional (kg en el caso de la masa y metros en el caso de la altura).
| masa | altura | energía potencial (J) |
|---|---|---|
| 4,5 kg | 9 m | |
| 10 kg | m | 9,8 |
| 5 g | 5,5 cm | |
| kg | 11 m | 2,7 |
| 1/2 kg | m | 2450 |
| kg | 47 mm | 2,3 |