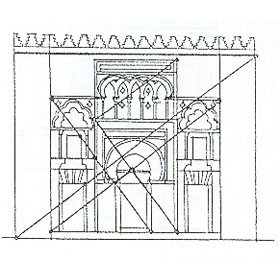
4.- Creando con phi
Iccanobif y Nietsnie se sorprendieron al descubrir que ya desde unas de las épocas más antiguas de la historia de este curioso planeta, el llamado antiguo Egipto, se trabajaba siguiendo las pautas de la proporción áurea.
Prueba de ello eran las famosas y misteriosas pirámides.
Posteriormente se le puso nombre propio al uso de esta proporción de forma reiterativa, Fidias y la Acrópolis de Atenas eran, más que un homenaje a los dioses, un homenaje a la razón… a la razón áurea.
Pero les intrigó aún más un "loco" de la divina proporción, uno de los mayores sabios de la historia humana, el gran Leonardo da Vinci. Él era un ejemplo de unión de ciencia, arte, invención, él era Phi con mayúsculas.
Pero no todo acababa ahí, aún en el arte abstracto, en las construcciones contemporáneas volvía a aparecer una y otra vez esta proporción.
Un ejemplo serían los cuadros de un tal Mondrian, un homenaje a la proporción áurea, un ejemplo de bella y estudiada "simplicidad".
Volvamos a nuestros ejemplos, primero uno arquitectónico: el Partenón. Todo él está repleto de la proporción áurea. Este edificio, hoy en forma de "ruinas" es uno de los más imitados a lo largo de la historia, ejemplo de equilibrio, sobriedad y grandeza arquitectónica.
En la siguiente imagen se muestran algunos de los rectángulos áureos que esconde entre sus viejas piedras:
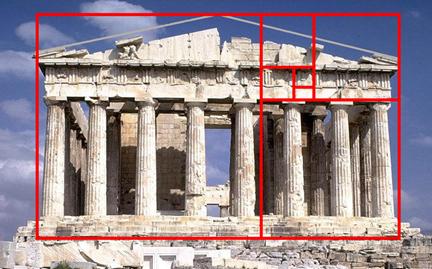
¿No recuerda a la forma matemática del Nautilus, la espiral?
Imágenes: Wikimedia commons
El otro ejemplo era el cuadro de la Gioconda o Mona Lisa de Leonardo da Vinci, quizá uno de los mayores tesoros del Museo del Louvre (Paris). Su rostro, su misteriosa sonrisa, su mirada, todo está envuelto en una serie de rectángulos áureos.
Un claro ejemplo de "estudiada naturalidad".
¿Cómo se podía construir un rectángulo áureo?
¿Cómo se podía saber que f= 
?
Para saber el proceso completo, observa atentamente la siguiente presentación:
Pregunta de Elección Múltiple
Imagen: Wikimedia Commons
Autoevaluación
En la presentación hemos visto que para descubrir el valor de phi es necesario el Teorema de Pitágoras, otro de los grandes matemáticos relacionado íntimamente con la proporción áurea. Vamos a ver si te has enterado bien, contestando a la siguiente cuestión:
¿Cuál es el valor de la hipotenusa de un triángulo rectángulo cuyos catetos miden respectivamente 3 cm y 4 cm?
|
7 cm
| |
|
25 cm
| |
|
5 cm
|
¡Cuidado
no has calculado bien!, has de sumar el valor del cuadrado de los
catetos, es decir, 3x3=9 y 4x4=16, dando como resultado 25 y después,
el valor de la hipotenusa será la raíz cuadrada de 25 o lo que es lo
mismo 5.
¡Muy
bien! Has sumado el valor del cuadrado de los catetos, es decir, 3x3=9
y 4x4=16, dando como resultado 25 y después, el valor de la hipotenusa
será la raíz cuadrada de 25 o lo que es lo mismo 5.En la siguiente presentación te mostraremos otros ejemplos de obras artística de distintas épocas en las que la composición se basa en al proporción áurea:
Pre-conocimiento
La unión entre Arte y Matemáticas no sólo se basa en la proporción áurea, existen infinidad de ejemplos que llevarían años de estudio.
En Andalucía se encuentran dos ejemplos de interés y belleza sin igual,
- La Proporción cordobesa (c) y
- Los frisos y mosaicos de la Alhambra de Granada.
Objetivos
Para saber más
En el siguiente enlace tienes una completa información sobre la proporción cordobesa. Si te gusta el tema puedes seguir navegando por esta misma unidad didáctica y descubrirás un poco más sobre la relación entre el Arte y las Matemáticas:
La proporción cordobesa o humana
Observa el siguiente vídeo de la serie "Más por menos" dedicado a los mosaicos de la Alhambra y su relación con las Matemáticas:
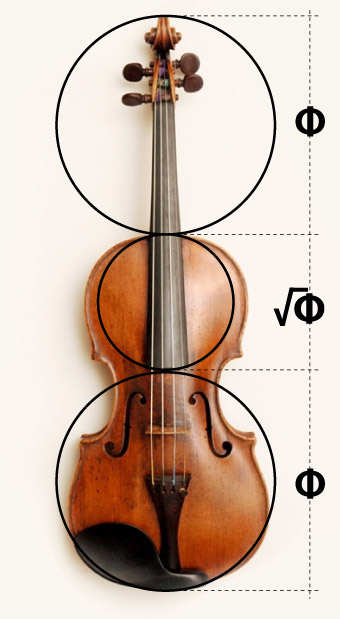
Imagen: Wikimedia commons
También se quedaron maravillados al descubrir la proporción áurea en el violín. ¿Magia?... No, la música, los instrumentos musicales y las matemáticas están íntimamente ligados. De hecho, la primera escala musical, "pentatónica" fue un invento pitagórico y... ¿te suena el término pentagrama...?
Las "efes" de los violines están colocadas siguiendo la razón áurea. Las sonatas de Mozart, la Quinta de Beethoven, Debussy, etc, tienen relación con la proporción áurea.
Objetivos
Para saber más:
Las relaciones entre los instrumentos musicales, las composiciones musicales y la proporción áurea son muy interesantes. En este enlace encontrarás la proporción áurea en distintos instrumentos musicales:
El número de oro en los instrumentos de cuerda.
Y aquí, el mismismo pato Donald, te explicará en un vídeo cómo se construye la escala pentatónica: