3.- ¿Hay alguna relación entre las magnitudes eléctricas?
Caso de estudio
Imagen: Wikimedia commons
¿Tú qué crees? Pues como ya vas conociendo bastante bien cómo "funcionan" los científicos, creemos que sospechas que sí, que tienen alguna relación. Y quizá sospeches más; probablemente sospeches que su relación se puede representar con una fórmula matemática.
Estás en lo cierto. Los científicos son así; buscan relaciones matemáticas entre las magnitudes y las expresan con una fórmula. Cuanto más sencilla es la fórmula que encuentran, tanto mejor, y eso es lo que sucede en este caso.
George Simon Ohm la descubrió y por eso la ley lleva su nombre; también en su honor se nombró la unidad de resistencia eléctrica, el ohmio.
La fórmula de la que te estamos hablando resume una de las relaciones más importantes de las que se cumplen en un circuito eléctrico. Esta relación se conoce con el nombre de ley de Ohm:
Actividad
El voltaje entre dos puntos de un circuito es siempre igual al producto de la intensidad de corriente que circula entre esos dos puntos por la resistencia eléctrica que haya entre ellos.
Dicho así, parece muy difícil, pero no lo es tanto si lo expresamos con una fórmula:
Actividad
|
VOLTAJE = INTENSIDAD x RESISTENCIA V = I x R |
Por eso a los científicos les gustan tanto las fórmulas. Son maneras muy sencillas de expresar relaciones que pueden ser muy complicadas.
La ley de Ohm se puede expresar también con otras fórmulas equivalentes a la anterior:
|
|
Caso de estudio
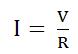
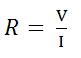
Observa en los siguientes ejemplos cómo se cumple la ley de Ohm:
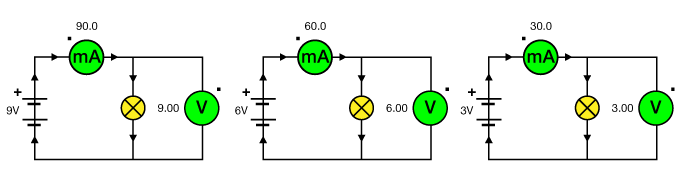
En los tres circuitos al amperímetro mide la intensidad de corriente que circula por la bombilla, y el voltímetro el voltaje entre sus extremos (que coincide con el de la pila en los tres casos).
Haz las cuentas necesarias y observa que al dividir lo que marca el voltímetro (el voltaje) entre lo que marca el amperímetro (la intensidad de corriente) obtenemos siempre el mismo valor.
Pregunta de Elección MúltipleAutoevaluación
1. El valor que has obtenido en las divisiones anteriores, ¿qué es?
|
La tensión suministrada por la pila.
| |
|
La resistencia de la bombilla.
| |
|
La carga eléctrica que circula por la bombilla.
|
Me parece que debes repasar otro poco.
¡Muy bien! Has acertado.
|
0,1 Ω.
| |
|
0,1 C.
| |
|
1000 C. | |
|
100 Ω.
|
Hay otra importante relación entre las magnitudes que hemos estudiado. Nos permite calcular la energía que suministra un generador (o que consume algún otro componente), si sabemos la intensidad de corriente que pasa por él y la tensión que hay entre sus extremos.
Nos referiremos a ella como la fórmula de la potencia, y es tan sencilla como la ley de Ohm.
Actividad
|
POTENCIA = VOLTAJE x INTENSIDAD P = V x I |
Pre-conocimiento
¡Atrévete!
En este enlace puedes ver cómo se utilizan estas fórmulas:
Ejemplos del Empleo de la Ley de Ohm y la Fórmula de la Potencia
Te recomendamos que, si tienes el programa simulador de circuitos, diseñes estos y otros circuitos similares y experimentes con ellos.
Como habrás comprobado en el enlace anterior, las cuentas que hay que hacer para aplicar estas fórmulas son muy sencillas. Tan sencillas que hasta funciona… la típica "regla de tres". Y es que estamos hablando de magnitudes directa o inversamente proporcionales.
Pre-conocimiento
¡Así es más fácil!
Pero por sencillas que sean unas cuentas, siempre es útil tener una herramienta que las haga solas. Prueba en el siguiente enlace a ver si te gusta ésta:
Actividad de Espacios en Blanco
Autoevaluación
Completa la tabla siguiente empleando la ley de Ohm y la fórmula de la potencia. (Escribe con dos cifras decimales y coma, los resultados que no sean números enteros)
| VOLTAJE (V) | INTENSIDAD (I) | RESISTENCIA (R) | POTENCIA (W) |
| 0,25 | 5 | ||
| 12 | 100 | ||
| 24 | 1,5 | 16 | |
| 220 | 2200 |
Objetivos
Para saber más…
Y no solo para eso, sino para repasar todo lo aprendido en el tema, comprender mejor los conceptos explicados y ... mucho más.
Esto es lo que puedes encontrar en el siguiente enlace. Se trata de una completa lección interactiva (completa pero muy fácil) que no tiene desperdicio; te recomendamos que no dejes de visitarla y de recorrer todos sus enlaces: